
VARIACIÓN DE LA PRESIÓN CON LA PROFUNDIDAD
Mientras que la presión atmosférica decrece con el incremento de la altitud, la presión de un líquido crece con la profundidad.
Supongamos un líquido en reposo para el cual la densidad es homogénea a través del mismo, lo que significa que es incompresible.
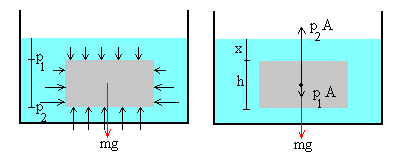
Como el líquido está en equilibrio, si analizamos una porción de líquido representado por el rectángulo sombreado en el interior del volumen en la figura, se cumple que la sumatoria de todas las fuerzas en la dirección vertical es cero.
Supongamos un líquido en reposo para el cual la densidad es homogénea a través del mismo, lo que significa que es incompresible.
Como el líquido está en equilibrio, si analizamos una porción de líquido representado por el rectángulo sombreado en el interior del volumen en la figura, se cumple que la sumatoria de todas las fuerzas en la dirección vertical es cero.

Teniendo en cuenta que
P = F/A entonces, F = PA
PA – P0 A – Mg = 0
Por otra parte, la densidad ρ = M/V, de donde M = ρ V
De ahí:
PA – P0 A – ρ V g = 0
siendo el volumen V = Ah, entonces al sustituir en la expresión anterior:
PA – P0 A – ρ Ah g = 0
PA – P0 A = ρ Ah g
Cancelando las áreas:
P - P0 = ρ g h
Esta ecuación es básica en la Estática de los Fluidos y, desde el punto de vista teórico, representa la variación de la presión con la profundidad h en el interior de un fluido. Nos dice que, la Presión P a una profundidad h por debajo de un punto en el fluido en el que la presión es P0, es mayor en una magnitud igual a ρ g h.
P = F/A entonces, F = PA
PA – P0 A – Mg = 0
Por otra parte, la densidad ρ = M/V, de donde M = ρ V
De ahí:
PA – P0 A – ρ V g = 0
siendo el volumen V = Ah, entonces al sustituir en la expresión anterior:
PA – P0 A – ρ Ah g = 0
PA – P0 A = ρ Ah g
Cancelando las áreas:
P - P0 = ρ g h
Esta ecuación es básica en la Estática de los Fluidos y, desde el punto de vista teórico, representa la variación de la presión con la profundidad h en el interior de un fluido. Nos dice que, la Presión P a una profundidad h por debajo de un punto en el fluido en el que la presión es P0, es mayor en una magnitud igual a ρ g h.
Si el líquido está abierto a la presión atmosférica, entonces la presión P0 en la superficie libre del líquido es la presión atmosférica, que es igual a 1 atm o 1.013 x 105 Pa.
En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: la presión
ejercida en cualquier lugar de un fluido encerrado e incompresible se
transmite por igual en todas las direcciones en todo el fluido, es
decir, la presión en todo el fluido es constante.
La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.
También podemos ver aplicaciones del principio de Pascal en las prensas hidraulicas.
Donde:
, presión total a la profundidad
medida en Pascales (Pa).
, presión sobre la superficie libre del fluido.
, densidad del fluido.
, aceleración de la gravedad.
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total (obviamente si el fluido fuera compresible, la densidad del fluido respondería a los cambios de presión y el principio de Pascal no podría cumplirse)
La prensa hidráulica es una máquina compleja semejante a un camión de Arquímides, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección S1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma (casi) instantánea a todo el resto del líquido. Por el principio de Pascal esta presión será igual a la presión p2 que ejerce el fluido en la sección S2, es decir:
con lo que, las fuerzas fueron siendo, siendo S1 < S2 :

y por tanto, la relación entre las fuerza resultante en el émbolo grande cuando se aplica una fuerza menor en el émbolo pequeño será tanto mayor cuanto mayor sea la relación entre las secciones:

La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:
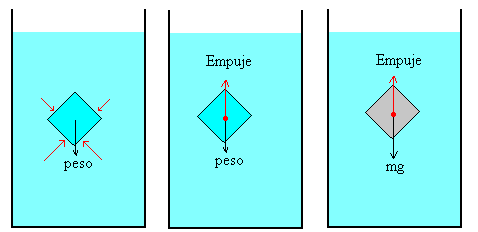
Porción de fluido en equilibrio con el resto del fluido.
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=rf·gV
El peso de la porción de fluido es igual al producto de la densidad del fluido rf por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.
La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.
También podemos ver aplicaciones del principio de Pascal en las prensas hidraulicas.
APLICACION DE PRINCIPIO DE PASCAL
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los liquidos. En esta clase de fluidos la densidad es prácticamente constante, de modo que de acuerdo con la ecuación:
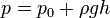 |
| p = p_0 + rho g h , |
Donde:
 |
| p , |
 |
| h , |
 |
| p_0 , |
 |
| rho , |
 |
| g , |
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total (obviamente si el fluido fuera compresible, la densidad del fluido respondería a los cambios de presión y el principio de Pascal no podría cumplirse)
PRENSA HIDRAULICA
La prensa hidráulica es una máquina compleja semejante a un camión de Arquímides, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección S1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma (casi) instantánea a todo el resto del líquido. Por el principio de Pascal esta presión será igual a la presión p2 que ejerce el fluido en la sección S2, es decir:
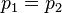 |
| p_1 = p_2 , |
con lo que, las fuerzas fueron siendo, siendo S1 < S2 :
 |
| F_1 = p_1 S_1 < p_1 S_2 = p_2 S_2 = F_2, |

y por tanto, la relación entre las fuerza resultante en el émbolo grande cuando se aplica una fuerza menor en el émbolo pequeño será tanto mayor cuanto mayor sea la relación entre las secciones:
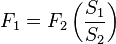 |
| F_1 = F_2 left( frac{S_1}{S_2} right) |

Principio de Arquímedes
El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:
- El estudio de las fuerzas sobre una porción de fluido en equilibrio con el resto del fluido.
- La sustitución de dicha porción de fluido por un cuerpo sólido de la misma forma y dimensiones.

Porción de fluido en equilibrio con el resto del fluido.
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=rf·gV
El peso de la porción de fluido es igual al producto de la densidad del fluido rf por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.
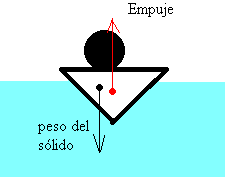 |
Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto. En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje. |
Ejemplo:
Supongamos un cuerpo sumergido de densidad ρ rodeado por un fluido de densidad ρf. El área de la base del cuerpo es A y su altura h.
La presión debida al fluido sobre la base superior es
p1= ρfgx, y la presión debida al fluido
en la base inferior es p2= ρfg(x+h).
La presión sobre la superficie lateral es variable y depende de la altura,
está comprendida entre p1 y p2.
Las fuerzas debidas a la presión del fluido sobre la
superficie lateral se anulan. Las otras fuerzas sobre el cuerpo son las
siguientes:
-
Peso del cuerpo, mg
-
Fuerza debida a la presión sobre la base superior, p1·A
-
Fuerza debida a la presión sobre la base inferior, p2·A
En el equilibrio tendremos que
mg+p1·A=
p2·A
mg+ρfgx·A= ρfg(x+h)·A
mg+ρfgx·A= ρfg(x+h)·A
o bien,
mg=ρfh·Ag
Como la presión en la cara inferior del cuerpo p2
es mayor que la presión en la cara superior p1, la
diferencia es ρfgh. El resultado es una fuerza hacia
arriba ρfgh·A sobre el cuerpo debida al fluido que le
rodea.
Como vemos, la fuerza de empuje tiene su origen en la
diferencia de presión entre la parte superior y la parte inferior del cuerpo
sumergido en el fluido.
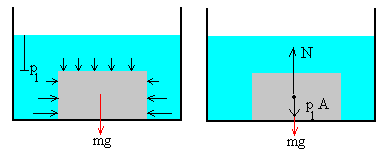
Con esta explicación surge un problema interesante y
debatido. Supongamos que un cuerpo de base plana (cilíndrico o en forma de
paralepípedo) cuya densidad es mayor que la del fluido, descansa en el fondo
del recipiente.
Si no hay fluido entre el cuerpo y el fondo del
recipiente ¿desaparece la fuerza de empuje?, tal como se muestra en la
figura

Si se llena un recipiente con agua y se coloca un
cuerpo en el fondo, el cuerpo quedaría en reposo sujeto por su propio peso
mg y la fuerza p1A que ejerce la columna de fluido
situada por encima del cuerpo, incluso si la densidad del cuerpo fuese menor
que la del fluido. La experiencia demuestra que el cuerpo flota y llega a la
superficie.


No hay comentarios:
Publicar un comentario