DINÁMICA ROTACIONAL

Momento angular de una partícula
Consideremos una partícula de masa m que se mueve con respecto a O con una velocidad v. Definimos una nueva magnitud vectorial, llamada momento angular de la partícula con respecto a O (L): |
 |
Sus unidades son: m2kg/s. El vector L es en cada instante perpendicular al plano formado por el vector posición y el vector velocidad; cuando la trayectoria es plana y el origen está contenido en el plano de la misma, L es perpendicular a dicho plano.
Teorema de conservación
Para determinar bajo qué condiciones L se mantiene constante, derivamos con respecto al tiempo: El primer término es nulo por tratarse del producto vectorial de dos
vectores paralelos, con lo que aplicando la definición de fuerza dada en
la segunda ley de Newton queda:
El primer término es nulo por tratarse del producto vectorial de dos
vectores paralelos, con lo que aplicando la definición de fuerza dada en
la segunda ley de Newton queda: Este producto vectorial se denomina momento o torque de una fuerza (τ) con respecto al origen O:
Este producto vectorial se denomina momento o torque de una fuerza (τ) con respecto al origen O:
 |
 |
el vector L será constante cuando su derivada sea nula. Esto constituye el Teorema de Conservación del Momento Angular:

Esta condición se cumple en dos casos:
- en el caso de una partícula libre, la fuerza a la que está sometida es nula por lo que no ejerce momento y por tanto se mueve con L constante, además de con momento lineal constantecuando el vector posición es paralelo a la fuerza, el producto vectorial es nulo por lo que L también es constante. Esto sucede en el caso de una fuerza central, es decir, que pasa siempre por un punto fijo: el momento angular de una partícula sometida exclusivamente a una fuerza central es constante. La fuerza gravitatoria es una fuerza central por lo que, por ejemplo, la Tierra se mueve con respecto al Sol con L constante. Si consultas la sección ¿sabías que..? de esta página verás qué consecuencias tiene este hecho.
- Momento angular de un sólido rígido
Las partículas de un sólido rígido en rotación alrededor de un eje fijo describen circunferencias centradas en el eje de rotación con una velocidad que es proporcional al radio de la circunferencia que describen

El momento angular de todas las partículas del sólido vale
En la figura se muestra el vector momento angular  de una partícula de masa mi cuya posición está dada
por el vector
de una partícula de masa mi cuya posición está dada
por el vector  y que describe una circunferencia de
radio Ri con velocidad vi.El módulo del vector
momento angular vale Li=rimivi
y que describe una circunferencia de
radio Ri con velocidad vi.El módulo del vector
momento angular vale Li=rimivi
Su proyección sobre el eje de rotación Z vale
Liz=ricos(90-q i)mivi, es decir,


La proyección Lz del vector momento angular a lo largo del eje de rotación es

El término entre paréntesis se denomina momento de inercia

El momento de inercia no es una cantidad característica como puede ser la masa o el volumen, sino que su valor depende de la posición del eje de rotación. El momento de inercia es mínimo cuando el eje de rotación pasa por el centro de masa.
En general, el vector momento angular  no tiene la dirección del eje de rotación, es decir, el vector momento
angular no coincide con su proyección Lz a lo largo del eje de
rotación. Cuando coinciden se dice que el eje de rotación es un eje principal de
inercia.Para estos ejes podemos relacionar el momento angular y la velocidad angular,
dos vectores que tienen la misma dirección, la del eje de rotación
no tiene la dirección del eje de rotación, es decir, el vector momento
angular no coincide con su proyección Lz a lo largo del eje de
rotación. Cuando coinciden se dice que el eje de rotación es un eje principal de
inercia.Para estos ejes podemos relacionar el momento angular y la velocidad angular,
dos vectores que tienen la misma dirección, la del eje de rotación

Rotacional y Lineal. Ejemplos
Se coloca una masa m, en una barra de longitud r y masa despreciable, y se le obliga a girar alrededor de un eje fijo. Si la masa se la libera de una orientación horizontal, podemos describir su movimiento en términos de fuerza y aceleración con la segunda ley de Newton para movimiento lineal, o como una rotación pura sobre el eje con la segunda ley de Newton para la rotación. Esto proporciona un marco para la comparación sobre un mismo sistema, de las cantidades lineales y de rotación. Este proceso nos lleva a la expresión del momento de inercia de una masa puntual.

Momento de Inercia: Varilla
Para una varilla uniforme de grosor despreciable, el momento de inercia sobre su centro de masa es
Momento de Inercia: Varilla
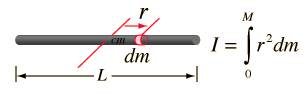
El cálculo del momento de inercia de una varilla sobre su centro de masa es un buen ejemplo de la necesidad del cálculo, frente a las propiedades de la distribución continua de masa. El momento de inercia de una masa puntual está dado por I = mr2, pero la varilla, se podría considerar que tiene un infinito número de masas puntuales y cada uno de ellos debe ser multiplicado por el cuadrado de su distancia al eje. La suma infinita se llama una integral. La forma general para el momento de inercia es:
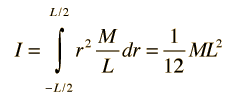
Mostrar detalles
Cálculo del Momento de la Varilla
El cálculo del momento de inercia para una varilla uniforme consiste en expresar cualquier elemento de masa dm en términos de elemento de distancia dr a lo largo de la varilla. Para realizar la integral, es necesario expresar todo lo que haya en la integral en términos de una variable, en este caso la variable de longitud r. Dado que el total de longitud L tiene masa M, entonces M / L es la proporción de masa sobre longitud y entonces el elemento de masa dm se puede expresar como se muestra. La integral es de tipo polinómico: 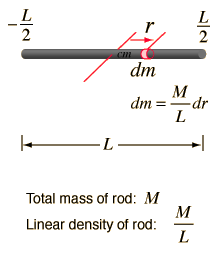
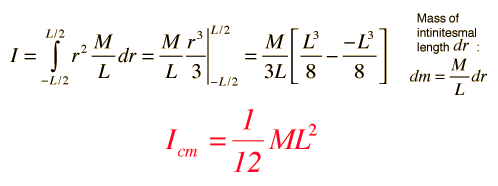
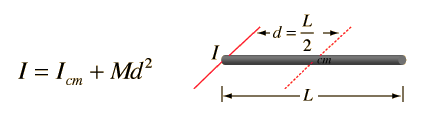
Momento de la Varilla sobre su Extremo
Una vez que se ha determinado el momento de inercia de un objeto sobre su centro de masa, el momento sobre cualquier otro eje se puede calcular, por medio del teorema de ejes paralelos: 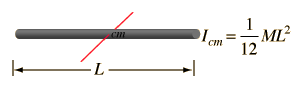
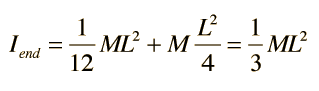
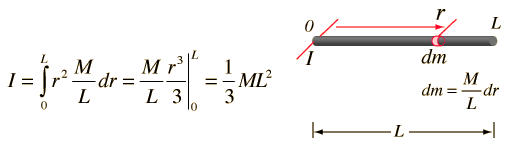
El momento de inercia refleja la distribución de masa de un cuerpo o de un sistema de partículas en rotación, respecto a un eje de giro. El momento de inercia sólo depende de la geometría del cuerpo y de la posición del eje de giro; pero no depende de las fuerzas que intervienen en el movimiento.
El momento de inercia desempeña un papel análogo al de la masa inercial en el caso del movimiento rectilíneo y uniforme. Es el valor escalar del momento angular longitudinal de un sólido rígido.
Ecuaciones del momento de inercia
Dado un sistema de partículas y un eje arbitrario, el momento de inercia del mismo se define como la suma de los productos de las masas de las partículas por el cuadrado de la distancia r de cada partícula a dicho eje. Matemáticamente se expresa como:
Para un cuerpo de masa continua (Medio continuo), se generaliza como: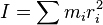
El subíndice V de la integral indica que se integra sobre todo el volumen del cuerpo. Se resuelve a través de una integral triple.
Este concepto desempeña en el movimiento de rotación un papel análogo al de masa inercial en el caso del movimiento rectilíneo y uniforme. La masa es la resistencia que presenta un cuerpo a ser acelerado en traslación y el Momento de Inercia es la resistencia que presenta un cuerpo a ser acelerado en rotación. Así, por ejemplo, la segunda ley de Newton: tiene como equivalente para la rotación:
tiene como equivalente para la rotación:
 es el momento aplicado al cuerpo.
es el momento aplicado al cuerpo. es el momento de inercia del cuerpo con respecto al eje de rotación y
es el momento de inercia del cuerpo con respecto al eje de rotación y es la aceleración angular.
es la aceleración angular.
La energía cinética de un cuerpo en movimiento con velocidad v es
 , mientras que la energía cinética de un cuerpo en rotación con velocidad angular ω es
, mientras que la energía cinética de un cuerpo en rotación con velocidad angular ω es 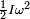 , donde
, donde  es el momento de inercia con respecto al eje de rotación.
es el momento de inercia con respecto al eje de rotación.La conservación de la cantidad de movimiento o momento lineal tiene por equivalente la conservación del momento angular
 :
: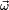 . Ambos vectores tienen la misma dirección si el eje de giro es un eje principal de inercia.
Cuando un eje es de simetría entonces es eje principal de inercia y
entonces un giro alrededor de ese eje conduce a un momento angular
dirigido también a lo largo de ese eje.
. Ambos vectores tienen la misma dirección si el eje de giro es un eje principal de inercia.
Cuando un eje es de simetría entonces es eje principal de inercia y
entonces un giro alrededor de ese eje conduce a un momento angular
dirigido también a lo largo de ese eje.Teorema de Steiner o teorema de los ejes paralelos
El teorema de Steiner (denominado en honor de Jakob Steiner) establece que el momento de inercia con respecto a cualquier eje paralelo a un eje que pasa por el centro de masa, es igual al momento de inercia con respecto al eje que pasa por el centro de masa más el producto de la masa por el cuadrado de la distancia entre los dos ejes:donde: Ieje es el momento de inercia respecto al eje que no pasa por el centro de masa; I(CM)eje es el momento de inercia para un eje paralelo al anterior que pasa por el centro de masa; M (Masa Total) y h (Distancia entre los dos ejes paralelos considerados).
La demostración de este teorema resulta inmediata si se considera la descomposición de coordenadas relativa al centro de masas C
 inmediata:
inmediata:donde el segundo término es nulo puesto que la distancia vectorial promedio de masa en torno al centro de masa es nula, por la propia definición de centro de masa.
El centro de gravedad y el centro de masa pueden no ser coincidentes, dado que el centro de masa sólo depende de la geometría del cuerpo, en cambio, el centro de gravedad depende del campo gravitacional en el que está inmerso dicho cuerpo.
Pasos para calcular el momento de inercia de áreas compuestas
- Dividir el área compuesta en varias partes que sean simples
- Determinar las áreas de las partes, designarlas por
 .
. - Determinar las coordenadas del centro de masas de estas partes
 con respecto a los ejes X e Y. Y calcular el cdm
con respecto a los ejes X e Y. Y calcular el cdm  de toda la figura formada por todas las áreas parciales anteriores.
de toda la figura formada por todas las áreas parciales anteriores. - Calcular las distancias de los cdm de cada área respecto al cdm total de la figura.
- Calcular los momentos de inercia de las partes respecto a sus ejes de centro de masas (que serán paralelos a x e y). Designar como:
 e
e  , para el área i-ésima.
, para el área i-ésima. - Calcular el momento de inercia de cada parte respecto a los ejes x e
y aplicando el teorema del eje paralelo, es decir, el teorema de
Steiner:
 y
y 
- Calcular los momentos de inercia del área compuesta a partir de los momentos anteriores:
 e
e 
Tensor de inercia de un sólido rígido
El tensor de inercia de un sólido rígido, es un tensor simétrico de segundo orden, que expresado en una base ortonormal viene dado por una matriz simétrica, cuyas componentes tensoriales son:Donde
 son las coordenadas cartesianas rectangulares.
son las coordenadas cartesianas rectangulares. , es el símbolo de Kronecker o delta de Kronecker definida como:
, es el símbolo de Kronecker o delta de Kronecker definida como: 
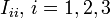 reciben el nombre de momento de inercia respecto al eje
reciben el nombre de momento de inercia respecto al eje  ,
y son las componentes diagonales del tensor. Las componentes del tensor
de inercia en un sistema de coordenadas cartesianas rectangulares son:
,
y son las componentes diagonales del tensor. Las componentes del tensor
de inercia en un sistema de coordenadas cartesianas rectangulares son:Y los tres productos de inercia según los mismos ejes:
Todas las formas anteriores pueden derivarse de la definición del tensor de momento de inercia haciendo :
 .
.
Donde la matriz es el tensor de inercia expresado en la base XYZ y
 es el vector paralelo al eje según el cual se pretende encontrar el momen
es el vector paralelo al eje según el cual se pretende encontrar el momen Ecuación del movimiento de rotación
El momento angular de un sólido rígido que rota con respecto a uno de sus ejes principales de inercia (que por el momento supondremos fijo con respecto a un sistema de referencia inercial) viene dado por:
 |
La variación del estado de rotación de un sólido viene determinada por la variación de su velocidad angular por lo que, si queremos describir el movimiento de rotación debemos encontrar una ecuación que nos permita calcular la aceleración angular del mismo.
Puesto que en la expresión del momento angular aparece la velocidad angular, derivándola obtendremos la aceleración angular:
 |
 |
 |
La segunda ley de Newton nos proporciona un modo de calcular la aceleración de una partícula (o del centro de masas de un sistema de partículas) conociendo las fuerzas que actúan sobre ella. La ecuación del movimiento de rotación de un sólido nos permite determinar su aceleración angular calculando el momento de las fuerzas externas que actúan sobre él.
Para que un cuerpo rote (para que tenga aceleración angular) no basta con que actúen fuerzas externas sobre él, sino que estas fuerzas han de tener momento resultante no nulo.
El papel que juega la masa de una partícula en la segunda ley de Newton (su inercia, es decir, la resistencia que opone a cambiar su estado de movimiento), lo desempeña ahora el momento de inercia.
Despejando α, se obtiene:
 |
El momento de inercia mide la resistencia que opone un cuerpo a variar su estado de movimiento de rotación.
De la ecuación anterior se deduce que el vector aceleración angular es paralelo a la resultante de los momentos de las fuerzas externas, del mismo modo que la aceleración de una partícula es paralela a la resultante de las fuerzas que actúan sobre ella.
Cuanto mayor sea el módulo de esta resultante, mayor será el módulo de la aceleración angular.
En el siguiente ejemplo se analiza el movimiento de rotación de una puerta utilizando la ecuación del movimiento de rotación.
 |
Si para abrirla aplicamos la fuerza directamente sobre la bisagra, la puerta no se abrirá, ya que en este caso: Para que la puerta se abra es necesario aplicar la fuerza a una cierta distancia de la bisagra, puesto que de este modo:  Cuanto mayor sea el módulo de r mayor será el momento de la fuerza F y por tanto mayor será la aceleración angular. Por eso es mas fácil abrir una puerta cuanto más lejos de la bisagra aplicamos la fuerza. |
ENERGIA DE ROTACIÓN
La energía cinética de un sistema es la suma de las energía cinética de las partículas que lo forman. Cuando un sólido rígido gira en torno a un eje que pasa por su centro de masas las partículas describen un movimento circular en torno a dicho eje con una velocidad lineal distinta según sea la distancia de la partícula al eje de giro pero todas giran con la misma velocidad angular ω, ya que en caso contrario el sólido se deformaría. La relación entre ambas velocidades aparece en la figura siguiente:
 |
Torque o Momento de Fuerza
1.
CUERPO RIGIDO: es aquel en que las posiciones relativas de sus
partículas no cambian. aunque éste sea sometido a la acción de fuerzas
externas, mantiene invariable su forma y volumen.
El movimiento general de un cuerpo rígido es una combinación de movimiento de traslación y de rotación. Para hacer su descripción es conveniente estudiar en forma separada esos dos movimientos.
ACCIÓN DE UNA FUERZA EN UN CUERPO RÍGIDO
El movimiento general de un cuerpo rígido es una combinación de movimiento de traslación y de rotación. Para hacer su descripción es conveniente estudiar en forma separada esos dos movimientos.
ACCIÓN DE UNA FUERZA EN UN CUERPO RÍGIDO

Una fuerza aplicada a un cuerpo rígido puede producir una
1 traslación

1 rotación
Ahora podemos comenzar a hablar de “TORQUE”
TORQUE O MOMENTO DE FUERZA:
“Torque” ( t) es la palabra que viene del latín torquere, torcer.
Es cuando se aplica una fuerza en algún punto de un cuerpo rígido, el cuerpo tiende a realizar un movimiento de rotación en torno a algún eje. La aplicación de una fuerza perpendicular a una distancia (brazo) del eje de rotación fijo produce un torque. Se manifiesta en la rotación del objeto.
El torque de una fuerza depende de la magnitud y dirección de F y de su punto de aplicación respecto de un origen O.
Torque es el producto de la magnitud de la fuerza perpendicular a la línea que une el eje de rotación con el punto de aplicación de la fuerza por la distancia (d) entre el eje de rotación y el punto de aplicación de la fuerza. Esto es:

Si la fuerza no es perpendicular al radio, sólo produce torque en la componente perpendicular a éste.



El torque puede ser POSITIVO O NEGATIVO.
Si el torque es en sentido contrario a las manecillas del reloj es positivo:
Si el torque es en sentido de las manecillas del reloj el torque es negativo:

FUERZAS QUE NO PRODUCEN TORQUE:
No produce torque una fuerza si es aplicada

*Paralela al brazo.
*En el eje de rotación.
Energía cinética de rotación
Las partículas del sólido describen circunferencias centradas en el eje de rotación con una velocidad que es proporcional al radio de la circunferencia que describen vi=w ·Ri . La energía cinética total es la suma de las energías cinéticas de cada una de las partículas. Esta suma se puede expresar de forma simple en términos del momento de inercia y la velocidad angular de rotaciónEcuación de la dinámica de rotación
Consideremos un sistema de partículas. Sobre cada partícula actúan las fuerzas exteriores al sistema y las fuerzas de interacción mutua entre las partículas del sistema. Supongamos un sistema formado por dos partículas. Sobre la partícula 1 actúa la fuerza exterior F1 y la fuerza que ejerce la partícula 2, F12. Sobre la partícula 2 actúa la fuerza exterior F2 y la fuerza que ejerce la partícula 1, F21.Por ejemplo, si el sistema de partículas fuese el formado por la Tierra y la Luna: las fuerzas exteriores serían las que ejerce el Sol ( y el resto de los planetas) sobre la Tierra y sobre la Luna. Las fuerzas interiores serían la atracción mutua entre estos dos cuerpos celestes.
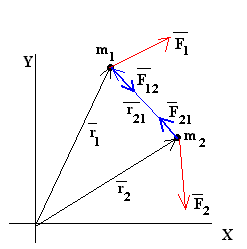 |
Para cada unas de las partículas se cumple que la variación del momento
angular con el tiempo es igual al momento de la resultante de las fuerzas que actúan
sobre la partícula considerada.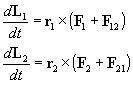 |
Como los vectores r1-r2 y F12 son paralelos su producto vectorial es cero. Por lo que nos queda
La derivada del momento angular total del sistema de partículas con respecto del tiempo es igual al momento de las fuerzas exteriores que actúan sobre las partículas del sistema.
Consideremos ahora que el sistema de partículas es un sólido rígido que está girando alrededor de un eje principal de inercia, entonces el momento angular L=I·w, la ecuación anterior la escribimos



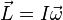



![I_{ij}= I_{ji} = \int_M \left[ \delta_{ij}r^2-x_ix_j \right] \ dm =
\int_V \rho(\mathbf r)\left[ \delta_{ij}r^2-x_ix_j \right] d^3\mathbf r](http://upload.wikimedia.org/math/5/8/e/58effcd418f6061dd7b80b13de8379b7.png)







No hay comentarios:
Publicar un comentario