Ecuación de continuidad
Ejemplo

Sin tomar en cuenta el cambio de las dimensiones de las tuberías por donde viaja el líquido:
El volumen del líquido que fluye es el mismo en la unidad de tiempo.
Ecuación de Bernoulli
La ecuación de Bernoulli, se puede considerar como una apropiada declaración del principio de la conservación de la energía, para el flujo de fluidos. El comportamiento cualitativo que normalmente evocamos con el término "efecto de Bernoulli", es el descenso de la presión del líquido en las regiones donde la velocidad del flujo es mayor. Este descenso de presión por un estrechamiento de una vía de flujo puede parecer contradictorio, pero no tanto cuando se considera la presión como una densidad de energía. En el flujo de alta velocidad a través de un estrechamiento, se debe incrementar la energía cinética, a expensas de la energía de presión.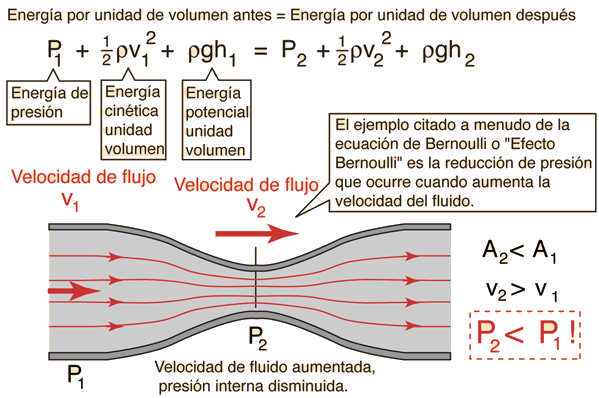
Cálculo de Bernoulli
El cálculo en el "mundo real", de la presión en un estrechamiento de un tubo, es dificil de hacer debido a las pérdidas por viscosidad, turbulencia, y presunciones que se deben hacer sobre el perfil de la velocidad (que afectan a la energía cinética calculada). El modelo de cálculo de aquí, asume un flujo laminar (sin turbulencia), tambien asume que la distancia del diámetro mayor al menor es suficientemente pequeña para despreciar las pérdidas por viscosidad y asume que el perfil de la velocidad sigue el del flujo laminar teórico. En concreto, esta asumiendo que la velocidad de la corriente efectiva es la mitad de la velocidad máxima, y que la densidad media de energía cinética está dada por un tercio de la densidad de energía cinética máxima.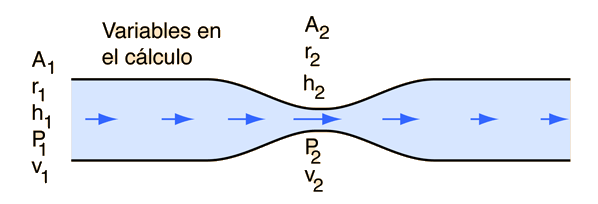

No hay comentarios:
Publicar un comentario